MA 01 - Základní pojmy

Matematická analýza, kapitola první, vymezení základních pojmů z oblasti logiky, množin a reálných čísel.

Logika

Základní způsob vyjadřování v matematice je pomocí výroků. Výrok může být buď pravdivý, má tedy hodnotu 1 anebo nepravdivý a má hodnotu 0. Negace tohoto výroku A se značí například non A anebo ¬A.

S výroky lze provádět čtyři základní operace – konjunkce, disjunkce, implikace a ekvivalence. Konjunkci (∧) odpovídá spojka a, disjunkci (∨) odpovídá spojka nebo či alternativa. Implikace je znázorněna znakem ⇒, ekvivalence pak ⇔.

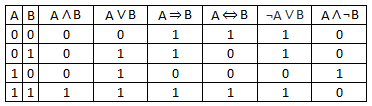
Znak pro konjunkci čteme et anebo a, znak pro disjunkci pak vel či nebo. Znak pro implikaci čteme implikuje a může být v češtině nahrazován několika způsoby A je postačující podmínkou pro B, nebo jestliže A, pak B, Znak pro ekvivalenci pak čteme A právě když B, nebo A tehdy, a jen tehdy když B (v angličtině býva často zkracován z if and only if na pouhé iff). Z tabulky je patrné, že implikace A⇒B je shodné s ¬A∨B. Poslední sloupec je pak negací implikace.

Jsou zavedeny dva kvantifikátory. Kvantifikátor obecný nebo též velký se značí ∀, někdy bývá značen ∏ nebo Λ, a čteme jej pro všechna. Kvantifikátor existenční nebo též malý se značí ∃, někdy bývá značen Σ nebo V, a čteme jej existuje nebo pro některé. Kvantifikátory lze řadit za sebou
Při negaci dochází ke změně obecného kvantifikátoru v existenční a obráceně. Pořadí zůstává zachováno. Negace výše uvedeného výroku by vypadala takto:

Jsou-li vedle sebe stejné kvantifikátory , mohou se zaměnit (∀x)(∀y) lze zapsat i (∀y)(∀x), neboť jde o ekvivalentní zápisy.

Množiny

Prvek a je prvkem množiny A značíme takto: a ∈ A. Také můžeme hovořit, že a patří do A nebo a náleží do A. Množina může mít konečný počet prvků a značíme ji takto: {a,b,c} Tato konečná množina je tvořena třemi prvky. Některé množiny značíme ustálenými symboly:

∅ – prázdná množina
– čísla přirozená (tj. celá kladná)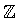
– čísla celá
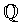– čísla racionální
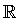– čísla reálná
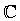– čísla komplexní

Sjednocení množin A a B vypadá následovně A ∪ B, průnik množin pak značíme takto A ∩ B. Je-li množina A podmnožinou množiny B, značíme takto: A ⊂ B. Vždy platí A ⊂ A a ∅ ⊂ A. Platí-li zároveň A ⊂ B a B ⊂ A, pak platí A = B. Množinu všech prvků množiny A, které zároveň nejsou prvky množiny B, značíme A \ B. Komplementem neboli doplňkem množiny A je pak ℜ \ A.

Kartézský součin A × B je množina uspořádaných dvojic a,b takových, že a ∈ A a b ∈ B. Je-li R ⊂ A × B, pak je R relace. Většinou místo (a,b) ∈ R značíme a R b (například a < b). Mnohdy pracujeme s relací na množině A čímž myslíme A × A.

Relace je tranzitivní, platí-li a R b a b R c, je také a R c. Relace je reflexivní, je-li a R a pro všechna a ∈ A. Pokud neexistuje žádný prvek, pro který by to platilo, pak je relace antireflexivní. Relace je symetrická, platí-li pro každou dvojici a R b ⇒ b R a. Relace je antisymetrická, pokud platí (a R b) ∧ (b R a) ⇒ (a = b).

Reflexivní, symetrickou a tranzitivní relaci na množině A nazýváme ekvivalencí na A. Reflexivní, antisymetrická a tranzitivní relace na množině A nazýváme částečné uspořádání na A. Pokud pro uspořádání vždy platí a R b nebo b R a, hovoříme o lineárním uspořádání (například ≤).

Reálná čísla

Obor reálných čísel je čtveřice , pro které platí níže uvedené axiomy. Za předpokladu, že a,b,c ∈ R, pak pro operaci sčítání (+) platí, že:

je komutativní, takže platí a + b = b + a
je asociativní, takže platí a + (b + c) = (a + b) + c
existuje (neutrální) nulový prvek 0 ∈ R, takový, že platí a + 0 = a
pro každé a existuje opačný prvek -a, takový, že platí a + (-a) = 0

Za předpokladu, že a,b,c ∈ R, pak pro operaci násobení (·) platí, že:

je komutativní, takže platí ab = ba
je asociativní, takže platí a(bc) = (ab)c
existuje (neutrální) jednotkový prvek 1 ∈ R, takový, že platí a · 1 = a
pro každé a existuje inverzní prvek a‾¹, takový, že platí a(a‾¹) = 1

Za předpokladu, že a,b,c ∈ R, pak pro operaci sčítání (+) a násobení (·) platí:

distributivní zákon, tedy platí a(b + c) = ab + ac

Za předpokladu, že a,b,c ∈ R, pak pro relaci menší než (<) platí, že:

je trichotomie, tedy nastává právě jeden z těchto případů: a < b, a = b, b < a
je tranzitivní, takže platí (a < b) ∧ (b < c) ⇒ a < c
(a < b) ⇒ a + c < b + c
(a < b) ∧ (0 < c) ⇒ ac < bc

Nyní můžeme definovat další relace:

a > b ⇔ b < a
a ≤ b ⇔ (a < b) ∨ (a = b)
a ≥ b ⇔ b ≤ a

Z výše uvedených axiomů vyplývá, že množina reálných čísel je uspořádané pole.

Číslo M ∈ R se nazývá horní závora (horní odhad) množiny A ⊂ R, pokud platí (∀x ∈ A)(x ≤ M). Je-li zároveň horní závora množiny i prvkem této množiny, hovoříme o maximu množiny A, tedy M = max A. Číslo m ∈ R se nazývá dolní závora (dolní odhad) množiny A ⊂ R, pokud platí (∀x ∈ A)(x ≥ m). Je-li zároveň dolní závora množiny i prvkem této množiny, hovoříme o minimu množiny A.

Množina A ⊂ R je shora omezená, pokud v R existuje alespoň jeden její horní odhad. Pokud existuje alespoň jeden její spodní odhad, pak je zdola omezená, pokud je má oba, pak je omezená.

Číslo S ∈ R je nejmenší horní odhad neboli supremum (sup A) množiny A ⊂ R, pokud platí:

(∀x ∈ A)(x ≤ S), tj. S je horní odhad A
(∀S‘ ∈ R)(∀x ∈ A)(x ≤ S‘) ⇒ S ≤ S‘, tj. S je supremum

Číslo s ∈ R je největší dolní odhad neboli infimum (inf A) množiny A ⊂ R, pokud platí:

(∀x ∈ A)(x ≥ s), tj. s je dolní odhad A
(∀s‘ ∈ R)(∀x ∈ A)(x ≥ s‘) ⇒ s ≥ s‘, tj. s je infimum

Poslední axiom, který popisuje množinu reálných čísel:

Každá neprázdná shora omezená množina A ⊂ R má supremum (v R), každá neprázdná zdola omezená množina A ⊂ R má infimum.

Množinu [a,b] nazýváme uzavřený interval, množinu (a,b) otevřený interval, množiny kombinující hranaté a kulaté závorky pak polouzavřené (polootevřené) intervaly. Hodnota b – a udává délku intervalu.

Absolutní hodnota |x| má vlastnosti |x| ≥ 0, |x| = 0 ⇔ x = 0, |xy| = |x|·|y|, |x+y| ≤ |x| + |y|.