Matematická analýza, kapitola šestá, řady, řady s kladnými členy, řady se střídavými znaménky, kritéria konvergence.
Pro posloupnost reálných čísel {ak} definujeme
jako částečný součet řady. Pokud dále platí, že
tedy existuje vlastní limita {sn}, pak hovoříme o tom, že řada ![]() konverguje k s. Ve všech ostatních případech říkáme, že řada diverguje (tedy s je rovno plus/mínus nekonečnu anebo součet neexistuje), je-li s = ±∞, pak diverguje k ±∞. Číslo s nazýváme součet řady, čísla ak pak členy řady a symboly nadsumační a podsumační nazýváme meze sčítání.
konverguje k s. Ve všech ostatních případech říkáme, že řada diverguje (tedy s je rovno plus/mínus nekonečnu anebo součet neexistuje), je-li s = ±∞, pak diverguje k ±∞. Číslo s nazýváme součet řady, čísla ak pak členy řady a symboly nadsumační a podsumační nazýváme meze sčítání.
Řady s kladnými členy
Definice 1 (srovnávací kritérium): Platí-li pro členy řad ∑an, ∑bn nerovnost an ≤ bn, pak říkáme, ře řada ∑an je minorantní řadou k řadě ∑bn a ∑bn je majorantní řadou k ∑an.
Příklad: Platí, že 0 < n ≤n!, a dále n! → +∞ a (n!)-1 → 0, pak je patrné, že řada
je konvergentní. Použijeme nepřesný ale názorný přepis řady, kde je patrná majorantní řada i odhad součtu:
Definice 2 (odmocninové kritérium): Řada ∑an konverguje, pokud pro číslo q, 0 ≤ q < 1 platí √an ≤ q.
Definice 3 (podílové kritérium): Řada ∑an konverguje, pokud pro číslo q, 0 ≤ q < 1 platí
Definice 4 (Raabeho kritérium): Řada ∑an konverguje, pokud pro číslo q, q > 1 platí
Řady se střídavými znaménky
Definice 5 (kritérium pro alterující řady): Řada ∑an konverguje, pokud pro alternující řadu a1 – a2 + a3 – a4 +… an ≥ 0 platí
Příklad: Jen si ukážeme řadu, jejíž součet je roven hodnotě π/4

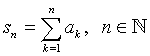

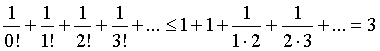
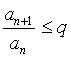

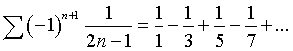


 Přihlaste se k odběru novinek.
Přihlaste se k odběru novinek.
5 comments
Skip to comment form
Awesome article post. Really looking forward to read more. Cool. Faun Randell James
You should take part in a contest for one of the most useful websites online. Lu Elwin Besnard
Supreme Court says Spanky can wear tutu and crotchless panties to work. Ula Micky Lowrie
Great article! This is the kind of info that are supposed to be shared around the web. Luella Farleigh Kellda
If you want to obtain much from this paragraph then you have to apply such methods to your won weblog. Roxane Joshia Neff