Matematická analýza, kapitola druhá, vymezení základních pojmů z oblasti zobrazení.
Zobrazení
Mějme X, Y neprázdné množiny, předpis f přiřazuje každému x ∈ X nějaký prvek y ∈ Y. Zpravidla tento prvek y značíme jako f(x). Každý takový předpis je pak nazýván zobrazení množiny X do množiny Y. Matematicky jej značíme buď f : X → Y, anebo f : x → f(x), x ∈ X. Obecně tedy máme X,Y ≠ ∅ a nechť f ⊂ X × Y, pro kterou platí:
- (∀x ∈ X)(∃y ∈ Y)((x,y) ∈ f)
- (((x,y1) ∈ f) ∧ ((x,y2) ∈ f)) ⇒ y1 = y2
Je zapotřebí si uvědomit, že zobrazení je vždy určeno na dané množině, proto f : x → x², x ∈ (0,1) a g : x → x², x ∈ (0,2), jsou dvě rozdílná zobrazení.
Pokud provedeme zobrazení pro množinu A ⊂ X, tedy x → f(x), x ∈ A, pak hovoříme o zúžení neboli restrikci. Podobně lze definovat rozšíření.
Mějme dány množiny X, Y, pro něž existuje zobrazení f : X → Y, pak říkáme, že
- D(f) = X je definiční obor f
- H(f) = {y ∈ Y; (∃x ∈ X)(y = f(x))} je obor hodnot f
Obecněji lze provést definici takto: Pro A ⊂ X, B ⊂ Y, máme:
- f(A) = {f(x); x ∈ A} ⊂ Y
- f‾¹(B) = {x ∈ X; f(x) ∈ B} ⊂ X
Obraz množiny A je f(A) a platí H(f) = f(X), vzor množiny B je pak f‾1(B) a platí D(f) = X = f‾1(Y).
Například pro f : x → 5, x ∈ (-5,2) je f([-1,1]) = {5}, f‾¹(3) = ∅, f‾¹(5) = (-5,2).
Zobrazení f : A → B, pro které existuje b ∈ B tak, že H(f) = {b}, se nazývá konstantní zobrazení. Jestliže pro f : A → A platí f(x) = x, x ∈ A, nazývá se pak f identické zobrazení na A, zjednodušeně pak identita na A.
Je-li f : X → Y a f(X) = Y, říkáme, že f zobrazuje X na Y; toto zobrazení se nazývá surjekce. Jesltiže má zobrazení f vlastnost (f(x1) = f(x2)) ⇒ (x1 = x2), jinak řečeno pro každé y ∈ Y existuje nejvýše jeden vzor f‾¹(y), nazývá se pak prosté zobrazení neboli injekce. Je-li pak zobrazení f zobrazením na a je-li současně prosté, nazýváme jej bijekce (vzájemně jednoznačné zobrazení) X na Y.
Nechť f : A → B, g : C → D jsou zobrazení a nechť platí f(A) ∩ C ≠ ∅. Potom f‾¹(B ∩ C) ≠ ∅ a lze definovat zobrazení
Někdy bývá značeno g ∗ f a značíme jej složené zobrazení ze zobrazení g a f.
Je-li f : N → B, nazýváme f posloupnost prvků množiny B.
Nechť pro n ∈ N existuje bijekce, která zobrazuje množinu {1,2,…,n} na A. Říkáme pak, že A je množina o n prvcích. Číslo n budeme označovat #A a nazývat jej mohutnost množiny neboli kardinalita, či kardinální číslo množiny A. Pro prázdnou množinu definujeme #∅ = 0. Pokud #A náleží do množiny nezáporných celých čísel (![]() ), pak tuto množinu nazýváme konečná množina. Ostatní množiny jsou pak nekonečné množiny. Existuje-li bijekce množiny N na A, pak říkáme, že množina A je nekonečná spočetná množina.
), pak tuto množinu nazýváme konečná množina. Ostatní množiny jsou pak nekonečné množiny. Existuje-li bijekce množiny N na A, pak říkáme, že množina A je nekonečná spočetná množina.
Každá podmnožina ![]() je spočetná. Neprázdná množina A je spočetná, právě když existuje prosté zobrazení f množiny A do
je spočetná. Neprázdná množina A je spočetná, právě když existuje prosté zobrazení f množiny A do ![]() . Neprázdná množina A je spočetná, právě když existuje zobrazení
. Neprázdná množina A je spočetná, právě když existuje zobrazení ![]() na A.
na A.
Jsou-li množiny A a B spočetné, je spočetná i množina A × B.
Množina všech celých čísel ![]() i racionálních čísel
i racionálních čísel ![]() je spočetná. Množina čísel reálných
je spočetná. Množina čísel reálných ![]() spočetná není.
spočetná není.
Jestliže je f : X → Y a Y ⊂ ![]() , pak nazýváme f reálnou fukncí. Obdobně jestliže je f : X → Y a Y ⊂
, pak nazýváme f reálnou fukncí. Obdobně jestliže je f : X → Y a Y ⊂ ![]() , pak nazýváme f komplexní funkcí. Je-li navíc X ⊂
, pak nazýváme f komplexní funkcí. Je-li navíc X ⊂ ![]() , nazýváme f reálná (komplexní) funkce reálné proměnné.
, nazýváme f reálná (komplexní) funkce reálné proměnné.
Jestliže je f : ![]() →
→![]() , pak nazýváme f posloupnost reálných čísel neboli posloupnost.
, pak nazýváme f posloupnost reálných čísel neboli posloupnost.
Funkce f : X →![]() je omezená na A, právě když existuje M > 0 takové, že platí:
je omezená na A, právě když existuje M > 0 takové, že platí:
Nechť f,g jsou reálné funkce definované na množině X. Potom součet, rozdíl, součin a podíl funkcí f,g jsou reálné funkce, které definujeme následujícím způsobem:

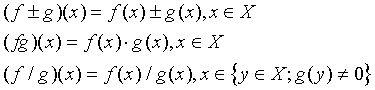


 Přihlaste se k odběru novinek.
Přihlaste se k odběru novinek.