KA01 - Základní definice

Úvodní kapitola teorie konečných automatů vymezí základní pojmy, se kterými se budeme dále setkávat.

Gramatika – soubor všech symbolů, znaků a pravidel, které je zapotřebí k vytváření vět.

Jazyk – obsahuje všechny věty, které lze vytvořit pomocí gramatiky. Jazyk tedy nemůže obsahovat nic, co není obsaženo v gramatice daného jazyka.

Automat – algoritmus, pomocí kterého zjistíme, zdali daná slova či věta patří do zkoumaného jazyka.

Definice 1: Abeceda Σ je konečná množina symbolů.

Definice 2: Libovolná posloupnost prvků abecedy Σ se nazývá slovo / řetězec α.

Definice 3: Délka řetězce |α| udává počet všech prvků daného slova.

Definice 4: Prázdný řetězec ε neobsahuje žádný prvek.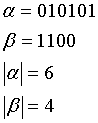
Definice 5: Pozitivní uzávěr abecedy je tvořen všemi kombinacemi, které je možné z daných prvků sestavit.

Definice 6: Uzávěr množiny Σ je spojením pozitivního uzávěru s prázdným řetězcem ε.
Definice 7: Formální jazyk L je podmnožina uzávěru množiny Σ.

Definice 8: Je-li množina L prázdná, hovoříme o prázdném jazyku, je-li konečná, pak o konečném jazyku a je-li nekonečná, tak o nekonečném jazyku.

Definice 9: Konečný (deterministický) automat je algoritmus, obsahující stavy, ve kterých se může nacházet, vstupní abecedu, přechodové funkce, pomocí nichž se dostáváme z jednoho stavu do dalšího, počáteční stav a seznam koncových stavů.

přičemž

Q = konečná neprázdná množina všech stavů
Σ = konečná neprázdná množina vstupní abecedy (symbolů)
δ = přechodové funkce pro jednotlivé stavy a vstupní symboly
q0 = počáteční stav, který zároveň náleží do Q
F = konečná neprázdná množina cílových stavů.

Definice 10: Zobecněná přechodová funkce δ konečného automatu A lze definovat rekurzivně za použití prázdného řetězce ε následovně:

Definice 11: Jazyk rozpoznávaný konečným automatem A, je ten jazyk, pro který platí:

Definice 12: Existuje-li konečný automat A, pro který platí vztah L(A) = L, pak je jazyk L nazýván jazykem rozpoznatelným konečným automatem A.

Definice 13: Konečný nedeterministický automat je algoritmus, obsahující stavy, ve kterých se může nacházet, vstupní abecedu, přechodové funkce, pomocí nichž se dostáváme z jednoho stavu do dalších, počáteční stavy a seznam koncových stavů. Automat může začínat ve více počátečních stavech a přechodová funkce je zobrazením do potenční množiny, tedy z jednoho stavu může automat přejít do libovolného počtu stavů (tedy i jen do jednoho nebo do žádného).

přičemž

Q = konečná neprázdná množina všech stavů
Σ = konečná neprázdná množina vstupní abecedy (symbolů)
δ = přechodové funkce pro jednotlivé stavy a vstupní symboly
I = konečná množina počátečních stavů
F = konečná neprázdná množina cílových stavů.

Definice 14: Zobecněná přechodová funkce δ konečného nedeterministického automatu A lze definovat jako sjednocení všech výsledků rekurzí za použití prázdného řetězce ε následovně:

Nedeterministický konečný automat přijímá slovo w, pokud platí

Definice 15: Jazyk rozpoznávaný konečným nedeterministickým automatem A, je ten jazyk, pro který platí:

Definice 16: Existuje-li konečný nedeterministický automat A, pro který platí vztah L(A) = L, pak je jazyk L nazýván jazykem rozpoznatelným nedeterministickým konečným automatem A.