Matematická analýza, kapitola čtvrtá, věty o limitách.
Základní věty
Věta 1: Každá posloupnost má nejvýše jednu limitu.
Věta 2: Nechť pro dvě posloupnosti an a bn, n ∈ ![]() existuje n1 ∈
existuje n1 ∈ ![]() takové, že an = bn, pro každé n > n1. Potom platí :
takové, že an = bn, pro každé n > n1. Potom platí :
- posloupnost an je omezená tehdy a jen tehdy, když je omezená i posloupnost bn
- posloupnost an má limitu a tehdy a jen tehdy, když posloupnost bn má limitu a (jedná se o reálné či komplexní číslo, anebo ±∞)
Věta 3: Limita posloupnosti (a omezenost) není závislá na konečném počtu jejích členů. (vyplývá to z věty 2.)
Věta 5:
Věta 6:
Věta 7: Každá konvergentní posloupnost je omezená.
Věta 8: Nechť lim an = +∞, pak je an omezená zdola a není omezená shora.
Věta 9: Nechť lim an = -∞, pak je an omezená shora a není omezená zdola.
Věta 10: Neklesající shora omezená posloupnost reálných čísel má limitu
Věta 11: Nerostoucí zdola omezená posloupnost reálných čísel má limitu
Věty o operacích s limity
Věta 12: Pokud jsou limity posloupnosti konvergentní, pak platí:
Příklad: Za použití výše uvedených vět spočítáme následující hodnotu limity
Jen pro připomenutí uvádím počítání s nekonečnem.
Operace s některými výrazy nejsou definovány. Nelze tedy vypočítat následující:
Pokud se setkáme se situací, že nám limita posloupnost vychází jako výraz, který není definován, musíme tvar původního výrazu převést tak, abychom dospěli k relevantnímu výsledku.
Příklad: Pokusíme se spočítat následující limitu posloupnosti:
Na první pohled je patrné, že čitatel výrazu se v nekonečnu přibližuje k plus nekonečnu a zároveň jmenovatel výrazu se v nekonečnu přibližuje k plus nekonečnu, takže by výsledek měl vypadat následovně:
Je patrné, že tento výraz není definován, proto budeme muset nejprve provést úpravu původního výrazu a tak dojít k výsledné limitě.
Je tedy patrné, že původní výraz má limitu posloupnosti 2,5.
Na závěr ještě uvedu limity pro goniometrické funkce: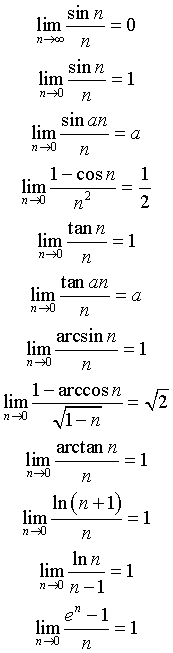
Příklad: Následující příklad ukazuje výpočet složitější limity.
Celý výraz vydělíme ![]() a získáme tedy následující tvar:
a získáme tedy následující tvar:
Již víme, že hodnota limity 1/n je rovna nule, stejně tak bude rovna nule i hodnota limity výrazu, který má ve jmenovateli mocninu n anebo v čitateli číselnou hodnotu. Je to způsobeno tím, že čím větší bude hodnota jmenovatele, tím menší bude hodnota daného výrazu. Navíc když se hodnota jmenovatele bude zvětšovat násobně (kvadraticky). Takže po provedení výpočtu do výrazu dostáváme nyní tento tvar:

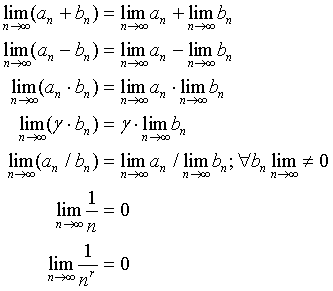
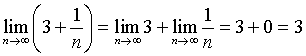
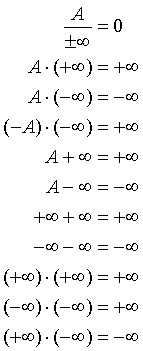
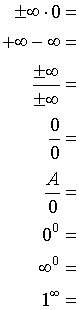
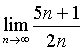
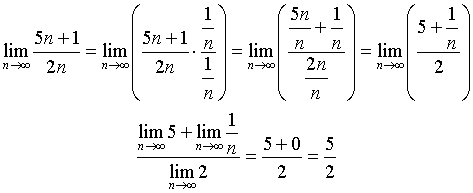
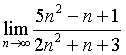
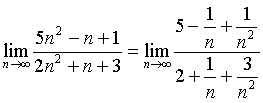
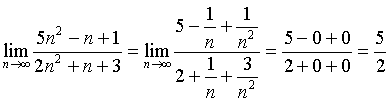


 Přihlaste se k odběru novinek.
Přihlaste se k odběru novinek.