Matematická analýza, kapitola třetí, posloupnosti, limita posloupnosti a její variace – vlastní, nevlastní, žádná.
Posloupnost
Posloupnost prvků množiny A je zobrazení f množiny ![]() do množina A. Zápis n → f(n), n ∈ N se pro posloupnosti nepoužívá, ale běžné jsou následující typy označení:
do množina A. Zápis n → f(n), n ∈ N se pro posloupnosti nepoužívá, ale běžné jsou následující typy označení:
Prvky označené aknazýváme členy neboli prvky posloupnosti.
Příklad:
Definice 1: Pokud pro posloupnost an platí nerovnost an ≥ an+1, nazýváme tuto posloupnost nerostoucí. Pokud platí nerovnost an ≤ an+1 nazýváme posloupnost neklesající. Posloupnost, která je nerostoucí anebo neklesající, nazýváme posloupnost monotónní. Posloupnost, která je zároveň nerostoucí anebo neklesající, nazýváme posloupnost konstantní.
Definice 2: Pokud pro posloupnost an platí nerovnost an > an+1, nazýváme tuto posloupnost klesající. Pokud platí nerovnost an < an+1 nazýváme posloupnost rostoucí.
Definice 3: Posloupnost an je aritmetická posloupnost s diferencí d, pokud platí an = an + d.
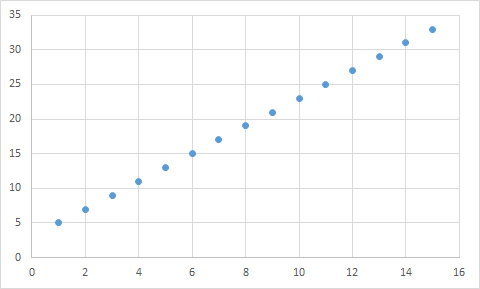
Příklad: Posloupnost pro an = 2n + 3 je aritmetická posloupnost s diferencí rovnou hodnotě 2. Hodnoty posloupnosti jsou totiž {5,7,9,11,13,…} a můžeme je graficky znázornit takto:
Definice 4: Posloupnost an je geometrická posloupnost s kvocientem q, pokud platí an = q · an.
Limita posloupnosti
Definice 5: ε-okolím bodu a nazýváme množinu všech řešení nerovnic a – ε < x < a + ε, přičemž ε > 0. Toto epsilonové okolí bodu a značíme U(a,ε) nebo Uε(a).
Definice 6: Číslo a ∈ ![]() nazýváme limitou posloupnosti {an}, pokud pro každé ε > 0 existuje takové k ∈
nazýváme limitou posloupnosti {an}, pokud pro každé ε > 0 existuje takové k ∈![]() , že pro všechna n ≥ k je
, že pro všechna n ≥ k je
Limitu posloupnosti pak značíme takto:
Limita posloupnosti zjednodušeně řečeno uvádí číslo, ke kterému se daná posloupnost neustále přibližuje.
Příklad: Pokusíme se stanovit limitu posloupnosti pro an = 1/n. Nejprve si na grafu uvědomme, jak jednotlivá hodnoty posloupnosti budou vypadat:
Na první pohled je patrné, že posloupnost se neustále přibližuje k hodnotě 0 (nicméně je patrné, že rovnice 1/n = 0 nikdy nebude platit). Nicméně limita posloupnosti v tomto případě bude nulová, neboť tato posloupnost se k nule blíží. Píšeme následovně:
Naopak limita posloupnosti výrazu n bude rovna nekonečnu.
Definici lze provést i pomocí kvantifikátorů:
![]() Definice limity tedy říká, že pro každé ε > 0 platí nerovnost |an-a| < ε pro skoro všechna n <
Definice limity tedy říká, že pro každé ε > 0 platí nerovnost |an-a| < ε pro skoro všechna n < ![]() .
.
Vlastní a nevlastní limita
Definice 7: Pokud an → a ∈ ![]() , pak říkáme, že {an} konverguje k a, nebo také že {an} je konvergentní anebo že konverguje. Jinými slovy existuje
, pak říkáme, že {an} konverguje k a, nebo také že {an} je konvergentní anebo že konverguje. Jinými slovy existuje ![]()
Definice 8: Limitu posloupnosti nazýváme vlastní limita, pokud je konvergentní.
Definice 9: Pokud není {an} konvergentní, pak je divergentní neboli diverguje.
Definice 10: Pokud an diverguje k plus nekonečnu (an → +∞) anebo an diverguje k mínus nekonečnu (an → -∞), hovoříme o nevlastní limitě.
Příklady: V předchozím příkladu vidíme limitu konvergentní k nule, takže se jedná o limitu vlastní. Naopak pokud budeme chtít zjistit limitu výroku n², zjistíme, že diverguje k plus nekonečnu. Na grafu pak průběh jednotlivých hodnot vypadá následovně:
Na první pohled je patrné, že posloupnost se neustále vzdaluje od nulové osy a bude se postupně blížit k plus nekonečnu. Zápis pak vypadá následovně:
Definice 11: Pokud posloupnost zároveň nemá ani vlastní limitu ani nevlastní limitu, hovoříme, že posloupnost nemá žádnou limitu.
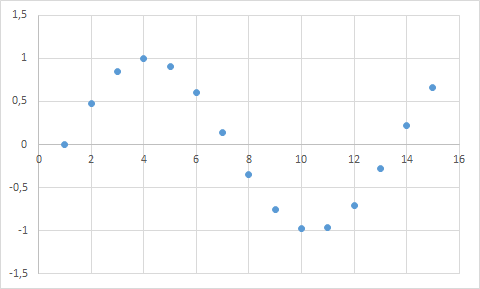
Příklad: Posloupnost výroku sin n nemá žádnou limitu a graficky ji můžeme znázornit takto:


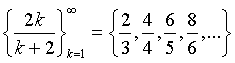

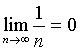



 Přihlaste se k odběru novinek.
Přihlaste se k odběru novinek.