Matematická analýza, kapitola šestá, řady, řady s kladnými členy, řady se střídavými znaménky, kritéria konvergence. Pro posloupnost reálných čísel {ak} definujeme jako částečný součet řady. Pokud dále platí, že
Category: Matematika
Pro 07
MA05 – Posloupnosti – příklady
Matematická analýza, kapitola pátá, příklady s řešením na výpočet limity posloupnosti. Řešené příklady: výpočet limity ve zlomku, limity s mocninou, limity s odmocninou, limity s kvadratickou rovnicí, limity s kubickou rovnicí, limity s kvartickou rovnicí, limity n-tých mocnin, limita faktoriálu, limita goniometrických funkcí (sinus, kosinus), limita logaritmu, limita eulerova čísla.
Pro 05
MA 04 – Posloupnosti – věty o limitách
Matematická analýza, kapitola čtvrtá, věty o limitách. Základní věty Věta 1: Každá posloupnost má nejvýše jednu limitu. Věta 2: Nechť pro dvě posloupnosti an a bn, n ∈ existuje n1 ∈ takové, že an = bn, pro každé n > n1. Potom platí : posloupnost an je omezená tehdy a jen tehdy, když je omezená i posloupnost bn posloupnost an má limitu a tehdy …
Lis 29
MA 03 – Posloupnosti – limita posloupnosti
Matematická analýza, kapitola třetí, posloupnosti, limita posloupnosti a její variace – vlastní, nevlastní, žádná. Posloupnost Posloupnost prvků množiny A je zobrazení f množiny do množina A. Zápis n → f(n), n ∈ N se pro posloupnosti nepoužívá, ale běžné jsou následující typy označení: Prvky označené aknazýváme členy neboli prvky posloupnosti. Příklad:
Lis 23
MA 02 – Základní pojmy – zobrazení
Matematická analýza, kapitola druhá, vymezení základních pojmů z oblasti zobrazení. Zobrazení Mějme X, Y neprázdné množiny, předpis f přiřazuje každému x ∈ X nějaký prvek y ∈ Y. Zpravidla tento prvek y značíme jako f(x). Každý takový předpis je pak nazýván zobrazení množiny X do množiny Y. Matematicky jej značíme buď f : X → Y, anebo f : x → f(x), x ∈ X. …
Lis 22
MA 01 – Základní pojmy
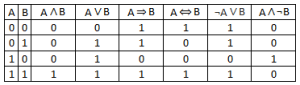
Matematická analýza, kapitola první, vymezení základních pojmů z oblasti logiky, množin a reálných čísel. Logika Základní způsob vyjadřování v matematice je pomocí výroků. Výrok může být buď pravdivý, má tedy hodnotu 1 anebo nepravdivý a má hodnotu 0. Negace tohoto výroku A se značí například non A anebo ¬A. S výroky lze provádět čtyři základní operace …
Kontakt
Své připomínky a náměty mi můžete psát na info@michaluvweb.cz.
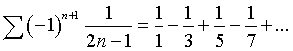
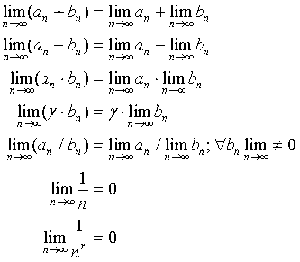
Přihlaste se k odběru novinek.