S konečnými automaty můžeme pracovat obdobně jako s množinami. Můžeme na ně aplikovat různé operace jako sjednocení, průnik, zřetězení, iterace, doplněk, zrcadlový obraz, kvocient, atd. Na úvod je zapotřebí si definovat třídu všech jazyků rozpoznatelných konečným automatem F.
Sjednocení dvou automatů A1 ∪ A2
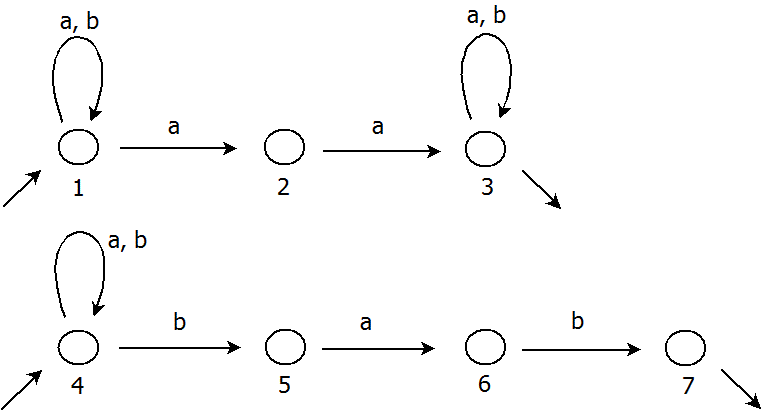
Sjednocením dvou automatů A1, rozpoznávajícího jazyk L1, a A2, rozpoznávajícího jazyk L2, vznikne automat A, který rozpoznává slova z jazyků L1 anebo L2. Vzpomeňme si na příklad automatu, který jsme použili v kapitole třetí – Převod NKA na DKA, který používá abecedu {a, b} a rozpoznává slova, která obsahují podslova „aa“ anebo slova, která končí na „bab“.
Jedná se vlastně o sjednocení automatu A1, který rozpoznává jazyk L1, jenž obsahuje podslova „aa“ a automatu A2, který rozpoznává jazyk L2, jenž obsahuje slova končící na „bab“. Stromový algoritmus pro sjednocení automatů pak vypadá takto:
- Kořen stromu tvoří počáteční stavy obou automatů.
- Patra stromu vytváříme aplikací přechodových funkcí obou konečných automatů.
- Výstupní množina stavů je tvořena všemi výstupními stavy automatu A1 a A2.
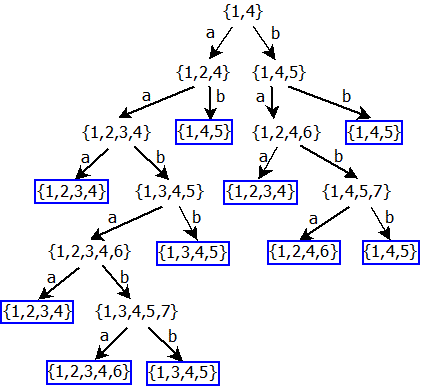
Nyní algoritmus pro sjednocení použijeme na výše uvedené dva automaty. Výsledkem pak bude následující stromový diagram:
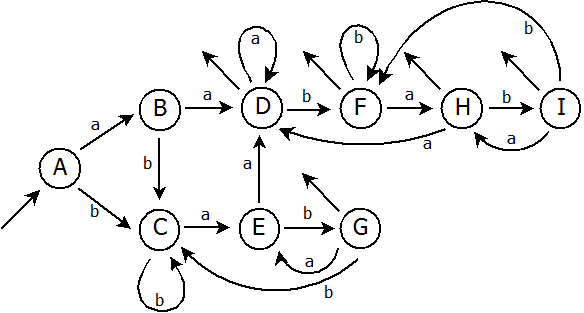
Přejmenujeme-li jednotlivé stavy tohoto automatu dle kapitoly třetí – Převod NKA na DKA, tak získáme výsledný sjednocený automat:
Průnik dvou automatů A1 ∩ A2
Průnikem dvou automatů A1, rozpoznávajícího jazyk L1, a A2, rozpoznávajícího jazyk L2, vznikne automat A, který rozpoznává slova z jazyků L1 a zároveň L2. Algoritmus bude obdobný sjednocení:
- Kořen stromu tvoří počáteční stavy obou automatů.
- Patra stromu vytváříme aplikací přechodových funkcí obou konečných automatů.
- Výstupní množina stavů je tvořena takovými podmnožinami, které obsahují alespoň jeden výstupní stav automatu A1 a zároveň alespoň jeden výstupní stav automatu A2.
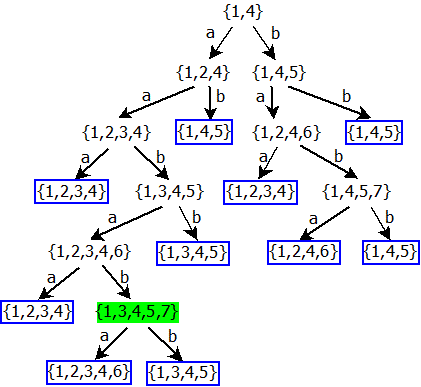
Použijeme výše uvedený příklad, a na něm si označíme všechny stavy, které obsahují jak výstupní stav prvního automatu, tak výstupní stav druhého automatu. Vzhledem k tomu, že první automat měl pouze jeden výstupní stav {3} a druhý automat měl taky jen jeden výstupní stav {7}, tak budeme hledat podmnožinu {3,7} v rámci všech stavů tohoto automatu.
Je patrné, že průnik těchto automatů má pouze jeden výstupní stav. Přejmenujeme jednotlivé stavy stejně jako u sjednocení automatů a dostaneme tento konečný automat:
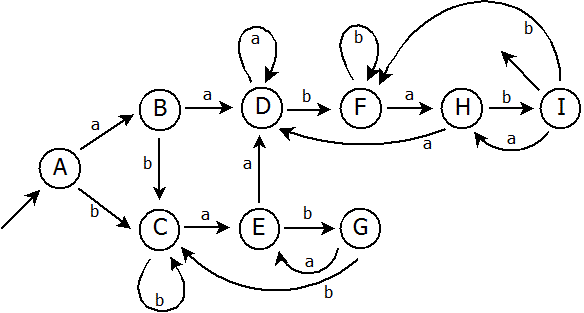
Chceme-li provést rychlý test pro ověření funkčnosti automatu, použijme slova, která automat rozpozná či nerozpozná. Například:
- baaaa – ACEDDD, nerozpoznáno
- abab – ACEG, nerozpoznáno
- aabab – ABDFHI, rozpoznáno
- babaa – ACEGED, nerozpoznáno
- babbab – ACEGCEG, nerozpoznáno
- babaabab – ACEGEDFHI, rozpoznáno
Doplněk automatu -A
Pro konečný automat A, který je schopen rozeznávat daná slova, existuje doplněk -A, který přesně tyto slova nerozpoznává a rozpoznává všechna ostatní. Dalo by se říci, že se jedná o nejjednodušší operaci, neboť dojde pouze k prohození stavů, které jsou výstupní a které ne. Algoritmus by pak mohl vypadat následovně:
- Vytvoříme nový automat A1 tak, že jej okopírujeme z automatu A, vyjma výstupních stavů.
- Pro každý stav automatu A, který není výstupní, zaznačíme u automatu A1 jako výstupní.
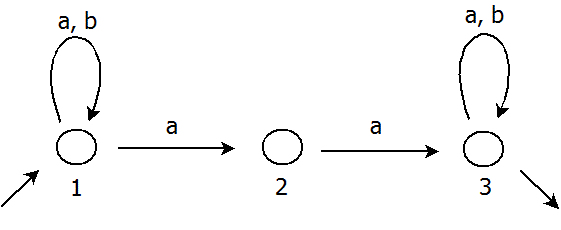
Jako příklad použijeme automat, který rozeznává slova, jenž obsahují podslova „aa“:
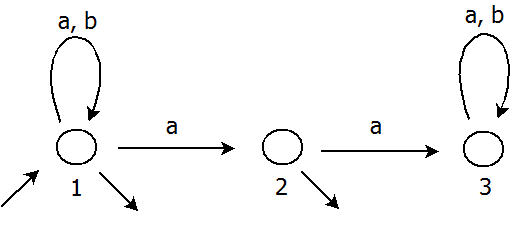
Vytvoříme kopii automatu bez výstupního stavu. Původní automat obsahoval jen jeden výstupní stav, a to stav 3. Tento stav se v novém automatu stane obyčejným stavem, naproti tomu stavy 1 a 2 se nově stanou výstupními. Výsledný automat -A vidíme zde:
Nyní můžeme udělat jednoduchou zkoušku. Náš automat by neměl rozpoznat žádná slova, která obsahují „aa“:
- aa – 123, nerozpoznáno
- baa – 1123, nerozpoznáno
- b – 11, rozpoznáno
- bb – 111, rozpoznáno
- ba – 112, rozpoznáno
- a – 12, rozpoznáno
- aab – 1233, nerozpoznáno
Další operace probereme už méně podrobněji, neboť budou vycházet z operací uvedených výše, anebo se bude jednat o jejich jednoduché obměny.
Rozdíl automatů A1 – A2
Algoritmus pro výpočet rozdílu dvou automatů si odvodíme z již známých operací. A1 – A2 jetotožné jako A1 ∩ -A2, takže nejprve vypočteme doplněk automatu A2 a pak provedeme průnik s automatem A1.
Zrcadlový obraz
Zrcadlový obraz tvoří slova jazyka čtená pozpátku. Sestrojení zrcadlového obrazu konečného automatu bude tedy jednoduché. Všechny přechody budou mít opačný směr a vstupy a výstupy budou obráceně.
Zřetězení automtatů A1•A2
Zřetězení automatů neboli součin automatů vytvoříme velice jednoduše. Stačí navázat výstupní stavy automatu A1 pomocí ε-přechodů na vstupní stavy automatu A2.
Iterace automatu
Pokud daný automat chceme iterovat, pak navážeme jeho výstupní stavy pomocí ε-přechodů na vstupní stavy. Značíme ![]() .
.
KA06 – Převod ZNKA na DKA



 Přihlaste se k odběru novinek.
Přihlaste se k odběru novinek.