KA03 – Převod NKA na DKA

Všechny nedeterministické konečné automaty se dají pomocí jednoduchého algoritmu převést na deterministické konečné automaty. Je zapotřebí pouze sjednotit vstupní stavy do jednoho deterministického vstupu a definovat nové vnitřní stavy, které budou odpovídat všem variacím z nedeterministické množiny.

Stromový algoritmus převodu NKA na DKA

1. Vytvoříme kořen stromu spojením všech možných počátečních stavů do jedné množiny.
2. Vytvoříme novou vrstvu stromu takovým způsobem, že pro každý stav z příslušné množiny předchozí vrstvy, vytvoříme novou množinu všech stavů, které jsou stavem následným po zadání příslušného znaku do automatu.
3. Pokud jsme v nově vytvořené vrstvě stromu sestavili množinu, která se již v předchozí hierarchii stromu objevila dříve, nebudeme ji již nijak dále rozvíjet.
4. Opakujeme krok číslo 2 tak dlouho, dokud existuje nová množina stavů, která se ještě ve stromové hierarchii neobjevila.
5. Označíme všechny podmnožiny, které obsahují výstupní stav původního automatu. Tyto množiny se stanou výstupními stavy nového automatu.
6. Jakmile je strom hotov, přejmenujeme jednotlivé podmnožiny na nové označení nového automatu a vytvoříme přechodové funkce.
7. Nyní můžeme vytvořit stavový diagram nově vzniklého deterministického konečného automatu.

Je patrné, že nově vzniklý deterministický automat je o mnoho složitější, než původní nedeterministický, neboť ten původní nemusel obsahovat všechny možné varianty vstupních symbolů. V praxi je někdy vhodnější při sestavování automatů vytvořit pro zadaný problém NKA, který pak jednoduše převedeme na DKA, než abychom pracně vytvářeli rovnou deterministický konečný automat.

Příklad

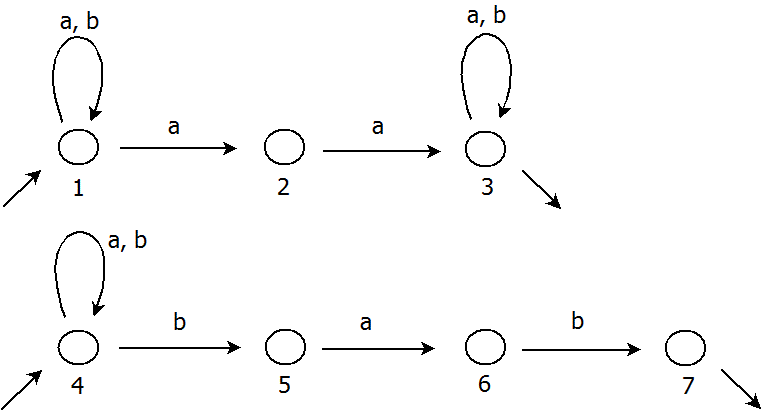
Mějme nedeterministický konečný automat z předchozí kapitoly, který používá abecedu {a, b} a rozpoznává slova, která obsahují podslova „aa“ anebo slova, která končí na „bab“. Jeho stavový diagram vypadá následovně:

Nyní začneme postupně vytvářet strom deterministického konečného automat. Nejprve si vytvoříme množinu všech vstupů: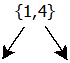

Nyní nalezneme všechny variace pro vstupní slovo a a b:

První vrstvu podmnožin máme vytvořenu, pustíme se do další:

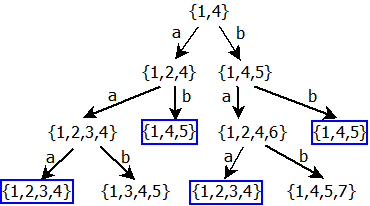
Z diagramu je patrné, že v nové vrstvě je množina {1,4,5}, a to dokonce hned dvakrát, která se nám již objevila v předchozí vrstvě. Proto ji označíme a nebudeme ji již více rozvádět:

Stejným způsobem pokračujeme dále:

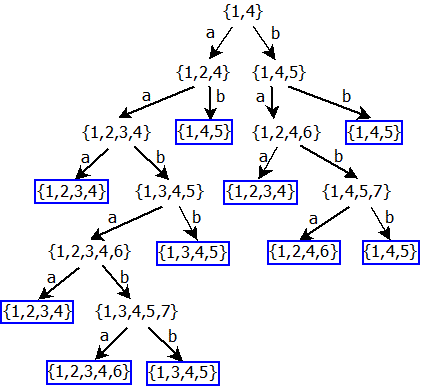
Takto dokončíme celý strom dle algoritmu a podmínky uvedené v bodě 4. Výsledek by měl vypadat následovně:

Nesmíme zapomenout označit všechny výstupní stavy.

Strom je hotov a nyní jej můžeme přejmenovat do nové struktury deterministického konečného automatu. Podmnožiny z této hierarchie nahradíme následovně: A = {1,4}, B = {1,2,4}, C = {1,4,5}, D = {1,2,3,4}, E = {1,2,4,6}, F = {1,3,4,5}, G = {1,4,5,7}, H = {1,2,3,4,6} a I = {1,3,4,5,7}. 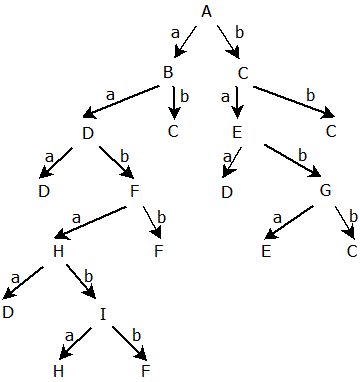Stanovíme přechodové funkce nového automatu pro všechny stavy:

Převod nedeterministického konečného automatu na deterministický konečný automat je hotov. Nyní si jej můžeme zobrazit pomocí stavového diagramu: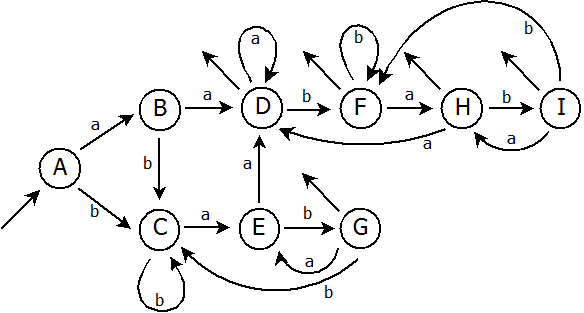 

Chceme-li provést rychlý test pro ověření funkčnosti automatu, použijme slova, která automat rozpozná či nerozpozná. Například:

• baaaa – prochází stavy ACEDDD, rozpoznáno
• abba – prochází stavy ABCCE, nerozpoznáno
• baba – prochází stavy ACEGE, nerozpoznáno
• abab – prochází stavy ABCEG, rozpoznáno
• babaa – prochází stavy ACEGED, rozpoznáno
• babbab – prochází stavy ACEGCEG, rozpoznáno
• babaabab – prochází stavy ABDFHDFHI, rozpoznáno

KA02 – Způsoby zápisu konečných automatů                        KA04 – Ekvivalentní automaty

Facebook

Twitter