Představíme-li si automat takový, že dokáže přecházet mezi jednotlivými stavy, aniž by načetl jakýkoliv vstupní symbol, hovoříme o zobecněném nedeterministickém konečném automatu, a tyto speciální stavy se nazývají ε-přechody.
Definice 1: Zobecněný nedeterministický konečný automat A je takový automat, pro nějž platí A = (Q, Σ, δ, I, F), kde Q je konečná množina všech stavů, Σ je konečná množina vstupních symbolů, δ je konečná množina přechodových funkcí, přičemž δ:Q×(Σ∪{ε}) → P(Q), I a F jsou konečné množiny vstupních a výstupních stavů.
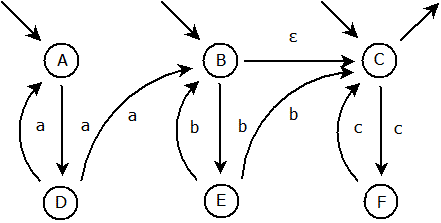
Následující příklad demonstruje zobecněný nedeterministický konečný automat, který je schopen rozpoznat jazyk L = {(aa)*(bb)*(cc)*}. Tento jazyk je reprezentován slovy, které postupně obsahují sudý (anebo nulový) počet znaků a, b a c.
Porovnáme-li sestavování NKA s ZNKA, pak je patrné, že návrh zobecněného automatu je jednodušší než nezobecněného, natož pak deterministického. Každý zobecněný nedeterministický konečný automat lze převést jak na NKA, tak i na DKA.
Algoritmus převodu ZNKA na NKA
- Pokud existují stavy, do kterých se lze přesunout pomocí ε-přechodu a jejich předchozí stav byl vstupní, pak i tyto stavy se nově stanou vstupními stavy.
- Pro stav který je vyústěním ε-přechodu, musíme jít v hierarchii o dva stavy zpět a vytvořit přímé propojení mezi tímto stavem a vyústěním ε-přechodu.
- Odstraníme ε-přechod.
- Pokud existuje další ε-přechod postupujeme krokem číslo 2.
Následující příklad demonstruje převod výše uvedeného zobecněného nedeterministického konečného automatu na nedeterministický konečný automat. Nejprve zjistíme všechny stavy, do kterých se lze přesunout ze vstupního stavu pomocí ε-přechodu. Tyto stavy jsou hned dva – B a C. Oba se tedy stanou vstupními stavy: 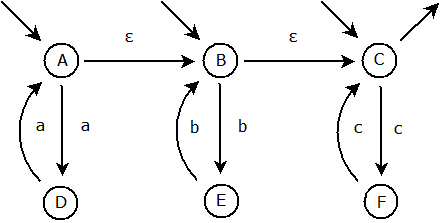
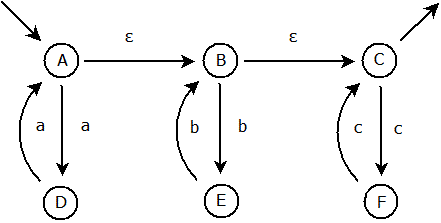
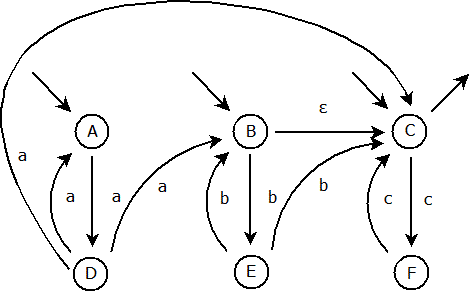
Dalším krokem bude vytvořením přímých spojení. První ε-přechod ústí do stavu B. Nalezneme v hierarchii dva stavy zpět, tedy 1. krok zpět je stav A, 2. krok zpět je stav D. Je tedy zapotřebí vytvořit přímé spojení stavů D a B:
Nyní jsme plně nahradili první ε-přechod a můžeme jej tedy odstranit:
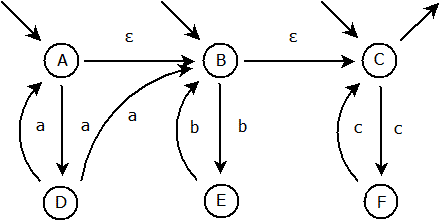
Náš ukázkový automat obsahuje další ε-přechod, který musíme vyřešit. Nejprve aplikujeme spojení obdobné tomu, které jsme vytvářeli u předchozího stavu. Vytvoříme přímé spojení stavů E a C:
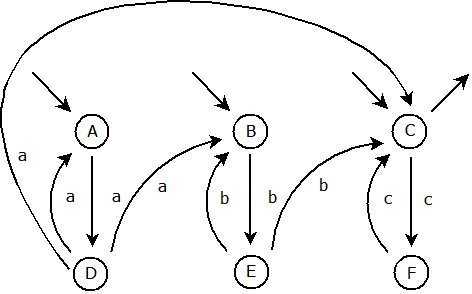
Zdálo by se, že nyní stačí odstranit ε-přechod a převod ZNKA na NKA je hotov. To je ale omyl. Přímým spojením stavů E a C jsme propojili situaci, kdy automat přijímá znaky bb, po nichž následuje stav cc. Náš automat ale umí rozpoznávat i slova obsahující znaky cc, které následují po znacích aa, což po vymazání posledního ε-přechodu tento nový automat neumí. Proč? Nesmíme zapomenout vytvářet nové přechody pro všechny existující varianty stavů, které jsou v hierarchii o dva stavy zpět po ε-přechodu. Nyní řešíme ε-přechod stavu C. Šli jsme zpětně přes stav B do stavu E a provedli jsme spojení E a C. Je zapotřebí jít i zpětně přes stav B do stavu D. Nyní tedy vytvoříme spojení D a C:
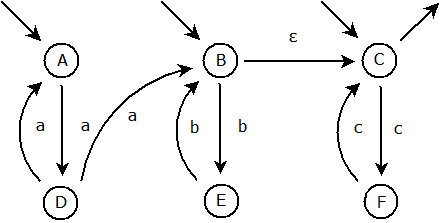
Nyní stačí odstranit zbývající ε-přechod a výsledný nedeterministický konečný automat je hotov:
Každý jazyk, který je rozpoznatelný ZNKA, je zároveň rozpoznatelný NKA i DKA.
KA04 – Ekvivalentní automaty KA06 – Převod ZNKA na DKA



 Přihlaste se k odběru novinek.
Přihlaste se k odběru novinek.