Zobecněný nedeterministický konečný automat lze převést přímo na deterministický konečný automat pomocí následujícího algoritmu. Je obdobný stromovému algoritmu převodu NKA na DKA. Nejprve si ale musíme vysvětlit, co je to E-funkce.
Definice 1: E-funkce E(q) přiřazuje každému stavu množinu stavů, které lze dosáhnout pomocí ε-přechodu.
Pokud máme například stavy A, B a C propojeny pomocí ε-přechodů, pak E(A) = {A, B, C}.
Algoritmus převodu ZNKA na DKA
- Vytvoříme kořen stromu spojením všech možných počátečních stavů do jedné množiny. Je zapotřebí zaspat i ty stavy, do kterých se dostaneme ze vstupního stavu pomocí ε-přechodu.
- Vytvoříme novou vrstvu stromu takovým způsobem, že pro každý stav z příslušné množiny předchozí vrstvy, vytvoříme novou množinu všech stavů, které jsou stavem následným po zadání příslušného znaku do automatu.
- Pokud jsme v nově vytvořené vrstvě stromu sestavili množinu, která se již v předchozí hierarchii stromu objevila dříve, nebudeme ji již nijak dále rozvíjet.
- Opakujeme krok číslo 2 tak dlouho, dokud existuje nová množina stavů, která se ještě ve stromové hierarchii neobjevila.
- Označíme všechny podmnožiny, které obsahují výstupní stav původního automatu. Tyto množiny se stanou výstupními stavy nového automatu.
- Jakmile je strom hotov, přejmenujeme jednotlivé podmnožiny na nové označení nového automatu a vytvoříme přechodové funkce.
- Nyní můžeme vytvořit stavový diagram nově vzniklého deterministického konečného automatu.
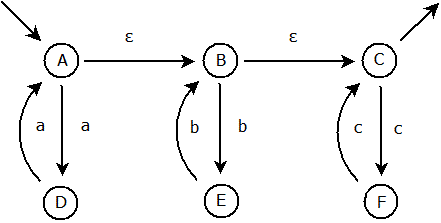
Jako příklad použijeme převod ZNKA z předchozí kapitolyt, který je schopen rozpoznat jazyk L = {(aa)*(bb)*(cc)*}. Tento jazyk je reprezentován slovy, které postupně obsahují sudý (anebo nulový) počet znaků a, b a c.
Určíme si E-funkce tohoto automatu. Stav A je propojen pomocí ε-přechodu se stavy B a C, takže E(A) = {A, B, C}. Stav B je pak propojen se stavem C, tedy E(B) = {B, C}. Ostatní stavy C, D, E a F již nejsou propojeny pomocí ε-přechodů, takž zde to bude již jednoduché. E(C) = {C}, E(D) = {D}, E(E) = {E} a E(F) = {F}.
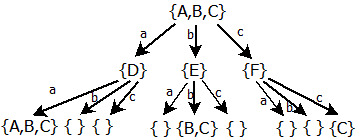
Strom začneme vytvářet vstupní vrstvou stavů, na kterou můžeme načítat symboly a, b a c, které nás posunou do stavů D, E a F:
Nyní budeme pokračovat další vrstvou. Načteme-li do stavu D symbol a, tak nás v původním automatu vrací do stavu A. V našem stromu ale musíme aplikovat E-funkce, takže místo stavu A uvedeme {A, B, C}. Pokud načítáme v určitém stavu symbol, který z daného stavu nikam nevede, ve stromu tento stav označíme { }.
Stavy, které již v hierarchii máme opakovaně, nebudeme dále rozvíjet a označíme je. Prázdné množiny rozvíjet nelze.
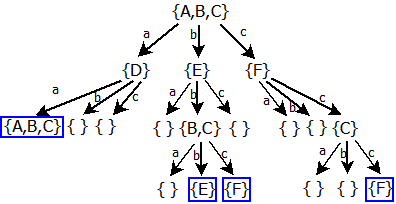
Nyní můžeme pokračovat dalším patrem stromu:
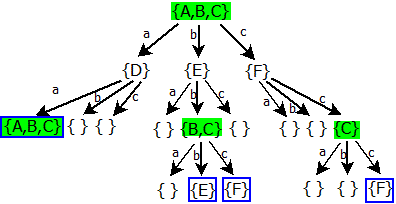
Označením výstupních stavů jsme dokončili náš strom:
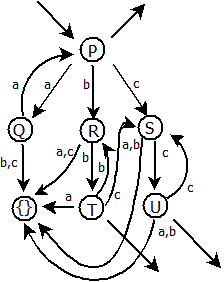
Nyní můžeme přejmenovat jednotlivé stavy a vytvořit stavový diagram. Použijeme následující názvosloví: P = {A, B, C}, Q = {D}, R = {E}, S = {F}, T = {B, C}, U = {C}.
Chceme-li provést rychlý test pro ověření funkčnosti automatu, použijme slova, která automat rozpozná či nerozpozná. Například:
- aabbcc – PQPRTSU, rozpoznáno
- accc – PQ{}, nerozpoznáno
- cc – PSU, rozpoznáno
- abc – PQ{}, nerozpoznáno
- ccaa – PSU{}, nerozpoznáno
- cba – PS{}, nerozpoznáno
- bbbbcc – PRTRTSU, rozpoznáno
KA05 – Zobecněné NKA KA07 – Operace s konečnými automaty





 Přihlaste se k odběru novinek.
Přihlaste se k odběru novinek.
1 comment
Uz som nasiel 🙂